Value at Risk (VaR) quantifies the maximum potential loss over a specified time horizon at a given confidence level, serving as a threshold for risk exposure. Conditional Value at Risk (CVaR) extends this by calculating the expected loss exceeding the VaR threshold, offering a more comprehensive assessment of tail risk. CVaR provides a better measure for portfolio optimization and risk management by capturing extreme loss scenarios often overlooked by VaR.
Table of Comparison
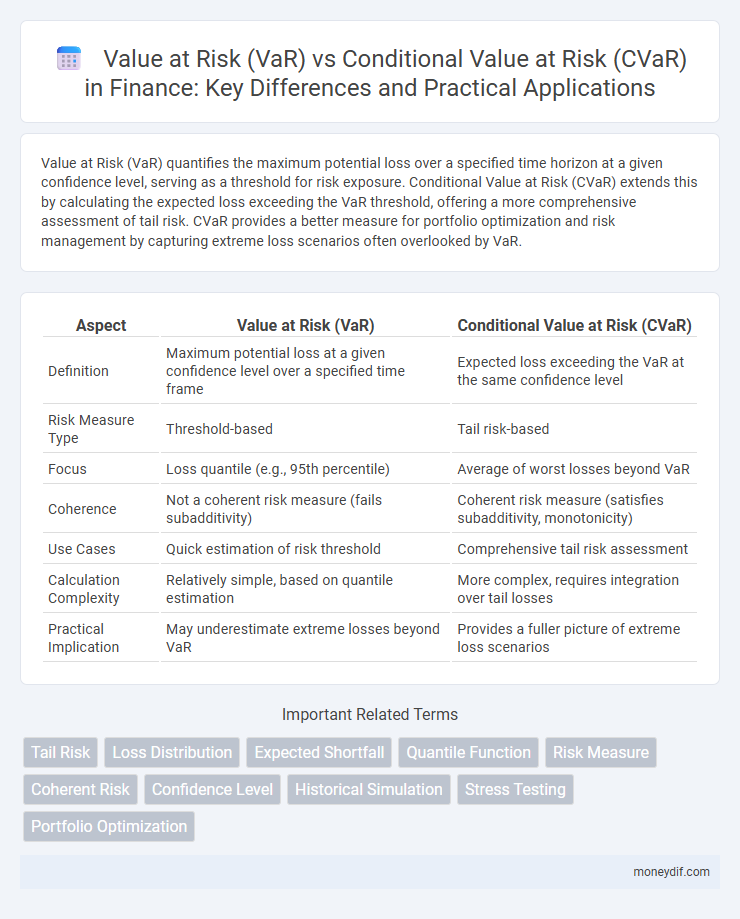
| Aspect | Value at Risk (VaR) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | Maximum potential loss at a given confidence level over a specified time frame | Expected loss exceeding the VaR at the same confidence level |
| Risk Measure Type | Threshold-based | Tail risk-based |
| Focus | Loss quantile (e.g., 95th percentile) | Average of worst losses beyond VaR |
| Coherence | Not a coherent risk measure (fails subadditivity) | Coherent risk measure (satisfies subadditivity, monotonicity) |
| Use Cases | Quick estimation of risk threshold | Comprehensive tail risk assessment |
| Calculation Complexity | Relatively simple, based on quantile estimation | More complex, requires integration over tail losses |
| Practical Implication | May underestimate extreme losses beyond VaR | Provides a fuller picture of extreme loss scenarios |
Introduction to Value at Risk (VaR) and Conditional Value at Risk (CVaR)
Value at Risk (VaR) quantifies the maximum expected loss over a specific time frame at a given confidence level, serving as a foundational risk metric in finance. Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss exceeding the VaR threshold, providing a more comprehensive assessment of tail risk. Both VaR and CVaR are critical for portfolio risk management, regulatory compliance, and capital allocation strategies.
Fundamental Concepts: VaR Explained
Value at Risk (VaR) quantifies the maximum expected loss over a defined period at a given confidence level, serving as a key risk metric in finance. It estimates potential portfolio losses without accounting for the magnitude of losses beyond the threshold, which can underestimate tail risk exposure. CVaR, or Conditional VaR, addresses this limitation by measuring the expected loss exceeding the VaR, providing a more comprehensive risk assessment in extreme market conditions.
Understanding Conditional Value at Risk (CVaR)
Conditional Value at Risk (CVaR) measures the expected loss given that losses exceed the Value at Risk (VaR) threshold, offering a more comprehensive risk assessment for tail events. CVaR captures the severity of extreme losses by averaging the worst-case losses beyond the VaR cutoff, making it particularly useful in portfolio optimization and risk management. Compared to VaR, CVaR provides a coherent risk metric that accounts for tail risk and improves decision-making under uncertainty.
Key Differences Between VaR and CVaR
Value at Risk (VaR) quantifies the maximum potential loss over a specified time frame at a given confidence level, but it does not provide information about losses beyond this threshold. Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss exceeding the VaR, offering a more comprehensive assessment of tail risk. CVaR is considered superior for risk management as it captures the severity of extreme losses, while VaR may underestimate risk in fat-tailed distributions.
Mathematical Formulation of VaR and CVaR
Value at Risk (VaR) is mathematically defined as the quantile of the loss distribution at a given confidence level a, representing the maximum potential loss not exceeded with probability a. Conditional Value at Risk (CVaR), also known as Expected Shortfall, calculates the expected loss exceeding the VaR threshold, expressed as the conditional expectation of losses beyond the VaR quantile. The formal formulation involves VaR_a = inf {x R : F_L(x) >= a} and CVaR_a = E[L | L >= VaR_a], where F_L is the loss distribution function and L denotes the loss variable.
Practical Applications in Risk Management
Value at Risk (VaR) measures the maximum potential loss over a given time frame at a specific confidence level, providing risk managers with a threshold for expected losses. Conditional Value at Risk (CVaR) extends this by estimating the average loss beyond the VaR threshold, making it crucial for assessing tail risk and extreme market scenarios. Financial institutions use CVaR to optimize portfolios and design stress tests that capture severe but plausible losses, enhancing capital allocation and regulatory compliance.
Advantages and Limitations of VaR
Value at Risk (VaR) provides a clear quantification of potential portfolio losses within a given confidence level, making it widely used for risk management and regulatory reporting. Its main advantage lies in simplicity and interpretability, facilitating communication of risk exposure to stakeholders. However, VaR limitations include its inability to capture tail risk beyond the quantile threshold, lack of subadditivity, and potential underestimation of extreme losses, making it less reliable in modeling rare but severe events.
Benefits and Drawbacks of CVaR
Conditional Value at Risk (CVaR) offers a more comprehensive risk assessment by capturing the expected losses exceeding the Value at Risk (VaR) threshold, providing better insights into tail risk exposure. CVaR improves risk management decisions through its coherent and subadditive properties, making it more suitable for portfolio optimization compared to VaR. However, CVaR can be computationally intensive and may require more complex estimation techniques, which can limit its practical implementation for large-scale or real-time risk analysis.
Choosing Between VaR and CVaR in Portfolio Risk Assessment
Choosing between Value at Risk (VaR) and Conditional Value at Risk (CVaR) in portfolio risk assessment depends on the risk sensitivity and accuracy required for tail risk evaluation. VaR provides a threshold loss value at a given confidence level but may underestimate extreme losses, while CVaR offers a more coherent risk measure by calculating the expected loss exceeding the VaR threshold. Portfolio managers often favor CVaR for its ability to capture tail risk more comprehensively, improving risk management and capital allocation decisions.
Future Trends in Financial Risk Measurement
Emerging trends in financial risk measurement emphasize integrating artificial intelligence and machine learning to enhance the accuracy of Value at Risk (VaR) and Conditional Value at Risk (CVaR) models. Advanced CVaR techniques, leveraging deep learning, provide superior tail risk assessment compared to traditional VaR, addressing extreme market scenarios more effectively. Regulatory frameworks increasingly demand stress testing and scenario analysis, promoting the adoption of dynamic risk measures that combine VaR and CVaR for comprehensive portfolio risk management.
Important Terms
Tail Risk
Conditional Value at Risk (CVaR) provides a more comprehensive assessment of tail risk by measuring the expected loss beyond the Value at Risk (VaR) threshold, capturing extreme downside scenarios that VaR alone may underestimate.
Loss Distribution
Conditional Value at Risk (CVaR) provides a more comprehensive loss distribution assessment than Value at Risk (VaR) by accounting for the tail losses beyond the VaR threshold.
Expected Shortfall
Expected Shortfall, also known as Conditional Value at Risk (CVaR), provides a risk measure that captures the average loss exceeding the Value at Risk (VaR) threshold, offering a more comprehensive assessment of tail risk in financial portfolios.
Quantile Function
The quantile function precisely determines Value at Risk (VaR) by identifying the loss threshold at a specified confidence level, while Conditional Value at Risk (CVaR) calculates the expected loss exceeding that VaR threshold, offering a more comprehensive risk assessment.
Risk Measure
Conditional Value at Risk (CVaR) provides a more comprehensive risk measure than Value at Risk (VaR) by estimating the expected loss exceeding the VaR threshold, thus capturing tail risk more effectively.
Coherent Risk
Coherent risk measures like Conditional Value at Risk (CVaR) provide more reliable portfolio risk assessment compared to Value at Risk (VaR) by satisfying subadditivity and convexity properties.
Confidence Level
Confidence Level determines the probability threshold at which Value at Risk (VaR) estimates potential losses, while Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR at the same confidence level.
Historical Simulation
Historical Simulation estimates Value at Risk (VaR) by using past market returns, while Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR threshold, providing a more comprehensive risk assessment.
Stress Testing
Stress testing evaluates financial risk by simulating extreme market conditions, complementing Value at Risk (VaR) and providing a more comprehensive risk assessment through Conditional Value at Risk (CVaR), which captures expected losses beyond the VaR threshold.
Portfolio Optimization
Conditional Value at Risk (CVaR) provides a more comprehensive risk assessment than Value at Risk (VaR) by estimating expected losses beyond the VaR threshold, enhancing portfolio optimization under extreme market conditions.
Value at Risk (VaR) vs Conditional Value at Risk (CVaR) Infographic
 moneydif.com
moneydif.com