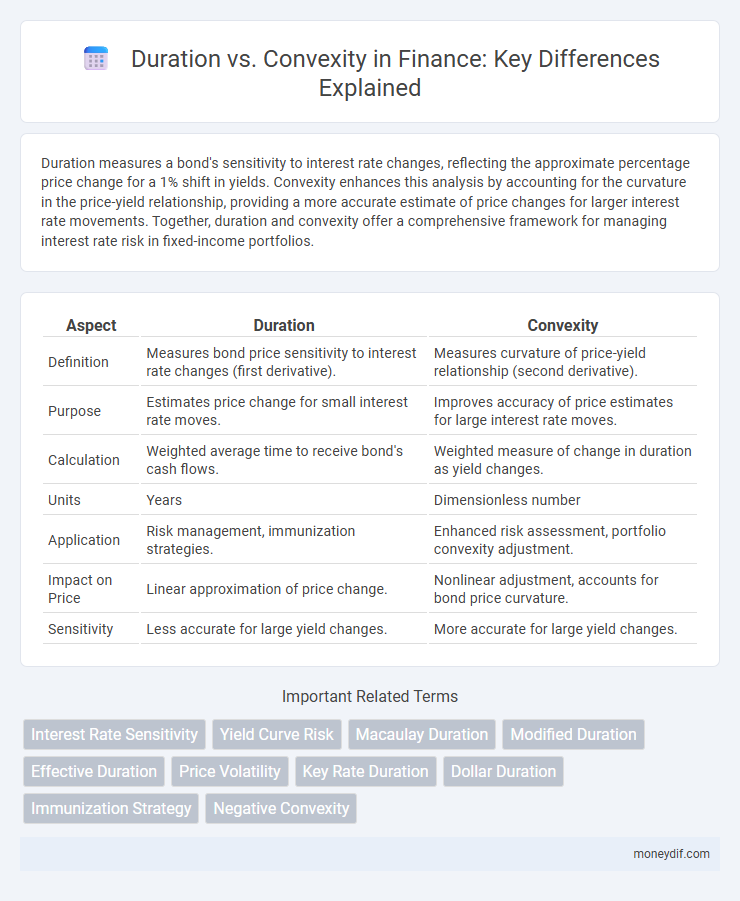
Duration measures a bond's sensitivity to interest rate changes, reflecting the approximate percentage price change for a 1% shift in yields. Convexity enhances this analysis by accounting for the curvature in the price-yield relationship, providing a more accurate estimate of price changes for larger interest rate movements. Together, duration and convexity offer a comprehensive framework for managing interest rate risk in fixed-income portfolios.
Table of Comparison
| Aspect | Duration | Convexity |
|---|---|---|
| Definition | Measures bond price sensitivity to interest rate changes (first derivative). | Measures curvature of price-yield relationship (second derivative). |
| Purpose | Estimates price change for small interest rate moves. | Improves accuracy of price estimates for large interest rate moves. |
| Calculation | Weighted average time to receive bond's cash flows. | Weighted measure of change in duration as yield changes. |
| Units | Years | Dimensionless number |
| Application | Risk management, immunization strategies. | Enhanced risk assessment, portfolio convexity adjustment. |
| Impact on Price | Linear approximation of price change. | Nonlinear adjustment, accounts for bond price curvature. |
| Sensitivity | Less accurate for large yield changes. | More accurate for large yield changes. |
Understanding Duration and Convexity in Bond Investing
Duration measures a bond's sensitivity to interest rate changes, reflecting the weighted average time to receive its cash flows, which helps investors estimate price volatility. Convexity captures the curvature in the price-yield relationship, providing a more accurate adjustment for large interest rate movements by accounting for the changing duration. By combining duration and convexity, bond investors can better predict price fluctuations and manage interest rate risk effectively.
Key Differences Between Duration and Convexity
Duration measures a bond's sensitivity to interest rate changes by estimating the percentage price change for a 1% change in yield, while convexity accounts for the curvature in the price-yield relationship, providing a more precise adjustment for large interest rate movements. Duration assumes a linear relationship between price and yield, whereas convexity captures the nonlinear effects, making it essential for assessing risk in volatile markets. Investors use duration for initial interest rate risk assessment and convexity to refine bond valuation and manage portfolio risk more accurately.
How Duration Measures Interest Rate Risk
Duration quantifies the sensitivity of a bond's price to changes in interest rates by estimating the approximate percentage price change for a 1% shift in yield. It represents the weighted average time to receive the bond's cash flows, serving as a linear risk measure for interest rate fluctuations. However, duration assumes a straight-line relationship and may underestimate risk for larger yield changes, where convexity becomes crucial to adjust for price curvature.
The Role of Convexity in Bond Price Sensitivity
Convexity measures the curvature in the relationship between bond prices and yields, providing a more accurate estimate of price sensitivity than duration alone, especially for large interest rate changes. Bonds with higher convexity exhibit less price decline when yields rise and greater price appreciation when yields fall, reducing interest rate risk for investors. Incorporating convexity into bond valuation models enhances risk management by capturing the nonlinear effects of interest rate movements on bond prices.
Calculating Duration: Methods and Formulas
Calculating bond duration involves methods such as Macaulay Duration and Modified Duration, both critical for assessing interest rate sensitivity. Macaulay Duration measures the weighted average time until a bond's cash flows are received, using the present value of cash flows divided by the bond price. Modified Duration adjusts Macaulay Duration by the bond's yield to maturity, quantifying the percentage change in bond price for a 1% change in yield, essential for risk management.
Interpreting Convexity: A Deeper Look
Convexity measures the curvature of a bond's price-yield relationship, providing a more accurate estimate of price changes than duration alone. Higher convexity indicates greater sensitivity to interest rate fluctuations, reducing the risk of price volatility for bond investors. Understanding convexity is essential for managing bond portfolios, as it helps in assessing interest rate risk and optimizing investment strategies.
Practical Applications of Duration and Convexity
Duration measures a bond's price sensitivity to interest rate changes, serving as a vital tool for immunizing portfolios against interest rate risk by matching asset and liability durations. Convexity refines this analysis by accounting for the curvature in the price-yield relationship, improving accuracy in estimating bond price changes for larger interest rate movements. Portfolio managers use both duration and convexity to optimize risk-adjusted returns and hedge effectively against market volatility.
Duration vs Convexity: Impact on Portfolio Management
Duration measures a bond's sensitivity to interest rate changes, estimating price volatility for small rate shifts, while convexity accounts for the curvature in the price-yield relationship, improving accuracy for larger rate movements. Portfolio managers utilize duration to gauge interest rate risk exposure and adjust asset allocations accordingly, whereas convexity helps refine risk assessment by capturing non-linear price changes and enhancing immunization strategies. Integrating both metrics optimizes bond portfolio management by balancing risk and return, enabling precise hedging against interest rate fluctuations.
Pros and Cons of Using Duration and Convexity
Duration measures a bond's sensitivity to interest rate changes, offering a straightforward estimate of price volatility, but it assumes a linear relationship and can be inaccurate for large interest rate movements. Convexity accounts for the curvature in the price-yield relationship, providing a more precise risk assessment for significant rate shifts, yet it requires more complex calculations and data inputs. Using both metrics simultaneously enhances risk management by balancing simplicity and accuracy in bond portfolio valuation.
Strategies to Optimize Bond Portfolios Using Duration and Convexity
Optimizing bond portfolios requires balancing duration to manage interest rate risk and convexity to capture price sensitivity to yield changes. Employing duration targeting strategies helps align portfolio sensitivity with liability or market benchmarks, while integrating convexity adjustments enhances risk assessment for large interest rate movements. Combining these metrics enables more precise hedging and improves portfolio resilience against fluctuating interest rates in dynamic financial environments.
Important Terms
Interest Rate Sensitivity
Interest rate sensitivity measures bond price changes where duration predicts linear price shifts and convexity accounts for curvature, enhancing accuracy for large interest rate movements.
Yield Curve Risk
Yield curve risk arises from changes in interest rates affecting bond prices, where duration measures price sensitivity to small yield changes and convexity accounts for the curvature in price-yield relationship for larger shifts.
Macaulay Duration
Macaulay Duration measures the weighted average time to receive a bond's cash flows and is a linear approximation of interest rate risk, while Convexity accounts for the curvature in price-yield relationship, providing a more accurate estimate of bond price sensitivity to interest rate changes.
Modified Duration
Modified Duration measures bond price sensitivity to interest rate changes, while Convexity accounts for the curvature in price-yield relationship, providing a more accurate risk assessment for large yield fluctuations.
Effective Duration
Effective duration measures a bond's price sensitivity to interest rate changes by accounting for embedded options, providing a more accurate assessment than traditional duration, while convexity quantifies the curvature of price-yield relationship to improve duration-based estimates.
Price Volatility
Price volatility increases with longer duration but is mitigated by higher convexity, as convexity reduces sensitivity to interest rate changes.
Key Rate Duration
Key Rate Duration measures a bond's sensitivity to interest rate changes at specific maturities, offering detailed risk insights that complement overall Duration and Convexity analyses.
Dollar Duration
Dollar Duration measures the price sensitivity of a bond to interest rate changes by combining Duration and the bond's market value, while Convexity accounts for the curvature in price-yield relationship, enhancing accuracy in bond price risk assessment.
Immunization Strategy
Immunization strategy balances duration and convexity to minimize interest rate risk by matching the portfolio's weighted average duration to the liability horizon while managing convexity to protect against non-parallel yield curve shifts.
Negative Convexity
Negative convexity occurs when bond prices increase less for a drop in yields than they decrease for an equivalent rise in yields, causing duration to understate interest rate risk in callable or mortgage-backed securities.
Duration vs Convexity Infographic
 moneydif.com
moneydif.com