Value at Risk (VaR) estimates the maximum potential loss within a given confidence level, providing a threshold for risk exposure, while Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR, offering a more comprehensive assessment of tail risk. CVaR captures the severity of losses in the worst-case scenarios, making it a vital tool for risk managers seeking to understand potential extreme losses beyond the VaR cutoff. Both metrics are essential in portfolio risk management, but CVaR delivers deeper insights for stress testing and risk mitigation strategies.
Table of Comparison
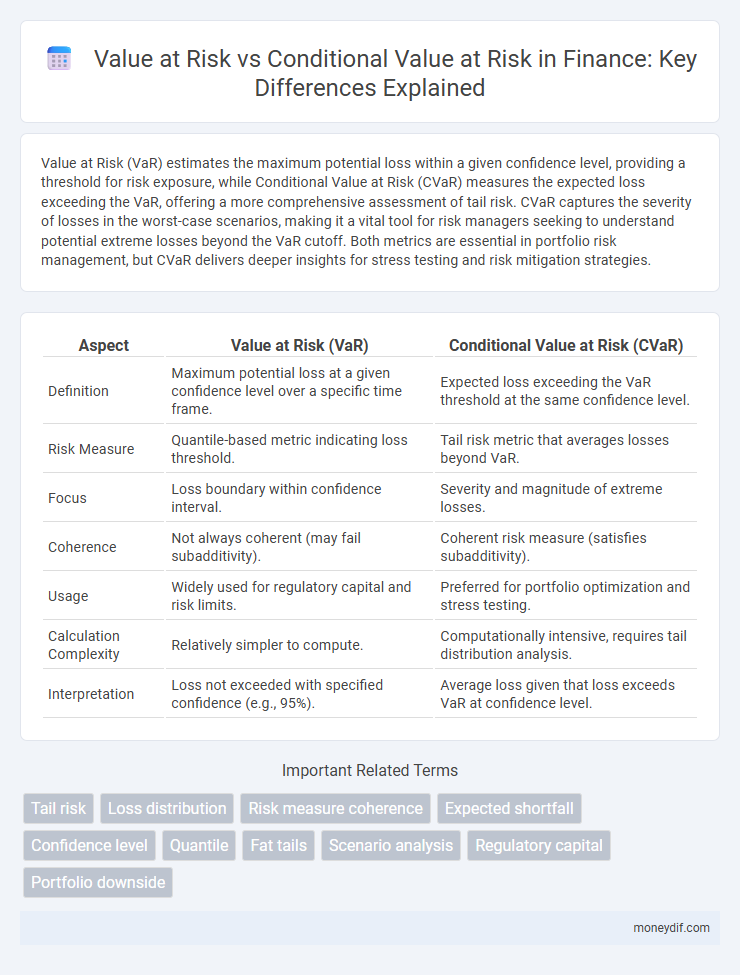
| Aspect | Value at Risk (VaR) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | Maximum potential loss at a given confidence level over a specific time frame. | Expected loss exceeding the VaR threshold at the same confidence level. |
| Risk Measure | Quantile-based metric indicating loss threshold. | Tail risk metric that averages losses beyond VaR. |
| Focus | Loss boundary within confidence interval. | Severity and magnitude of extreme losses. |
| Coherence | Not always coherent (may fail subadditivity). | Coherent risk measure (satisfies subadditivity). |
| Usage | Widely used for regulatory capital and risk limits. | Preferred for portfolio optimization and stress testing. |
| Calculation Complexity | Relatively simpler to compute. | Computationally intensive, requires tail distribution analysis. |
| Interpretation | Loss not exceeded with specified confidence (e.g., 95%). | Average loss given that loss exceeds VaR at confidence level. |
Introduction to Value at Risk (VaR) and Conditional Value at Risk (CVaR)
Value at Risk (VaR) quantifies the maximum potential loss of a portfolio over a defined time frame at a given confidence level, serving as a fundamental risk metric in finance. Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss beyond the VaR threshold, capturing tail risk more effectively. Financial institutions employ both VaR and CVaR to enhance risk management by quantifying potential extreme losses and improving capital allocation strategies.
Key Definitions: VaR vs CVaR
Value at Risk (VaR) quantifies the maximum potential loss in a portfolio over a specified time frame at a given confidence level, typically ignoring losses beyond this threshold. Conditional Value at Risk (CVaR), also known as Expected Shortfall, calculates the average loss exceeding the VaR, providing a more comprehensive assessment of tail risk. CVaR addresses the limitations of VaR by capturing the severity of extreme market movements, making it a preferred metric for risk management and regulatory compliance.
Mathematical Formulations of VaR and CVaR
Value at Risk (VaR) is mathematically defined as the quantile of the loss distribution at a specified confidence level, representing the maximum expected loss over a target horizon under normal market conditions. Conditional Value at Risk (CVaR), also known as Expected Shortfall, is formulated as the expected loss exceeding the VaR threshold, providing a coherent risk measure by capturing tail risk beyond the VaR quantile. The mathematical distinction lies in VaR being a quantile function \( \text{VaR}_\alpha = \inf \{ x : P(L \leq x) \geq \alpha \} \), while CVaR is the conditional expectation \( \text{CVaR}_\alpha = E[L \mid L \geq \text{VaR}_\alpha] \), making CVaR sensitive to the severity of losses in the tail of the distribution.
Assumptions and Limitations of VaR
Value at Risk (VaR) assumes normal distribution of asset returns and stable market conditions, which can underestimate risk during extreme events. VaR's limitation lies in its inability to capture tail risk beyond the specified confidence level, often ignoring the severity of losses in worst-case scenarios. Conditional Value at Risk (CVaR) addresses this by focusing on the expected loss given that the loss exceeds the VaR threshold, providing a more comprehensive risk assessment.
Why CVaR Matters: Beyond the Risk Threshold
Value at Risk (VaR) quantifies the maximum potential loss over a specific period at a given confidence level, but it fails to capture the magnitude of losses beyond that threshold. Conditional Value at Risk (CVaR) addresses this limitation by measuring the expected loss exceeding the VaR, providing a more comprehensive assessment of tail risk. Financial institutions prioritize CVaR to enhance risk management strategies and improve capital allocation under extreme market conditions.
Comparing Risk Measurement Accuracy: VaR vs CVaR
Value at Risk (VaR) quantifies the maximum potential loss over a specified time frame at a given confidence level, yet it often underestimates tail risk due to its inability to account for losses beyond the threshold. Conditional Value at Risk (CVaR), also known as Expected Shortfall, improves risk measurement accuracy by calculating the expected loss given that the loss exceeds the VaR, thus capturing tail-end risks more effectively. Empirical studies demonstrate that CVaR provides a more coherent and sensitive risk metric, particularly useful for portfolios with fat-tailed distributions or during extreme market conditions.
Real-World Applications: VaR and CVaR in Portfolio Management
Value at Risk (VaR) quantifies the maximum expected loss over a specific time frame at a given confidence level, making it a foundational risk metric in portfolio management. Conditional Value at Risk (CVaR), also known as Expected Shortfall, provides a more comprehensive risk assessment by estimating the average loss exceeding the VaR threshold, thus capturing tail risk more effectively. Portfolio managers utilize CVaR to optimize asset allocation by minimizing severe loss scenarios, while VaR remains essential for regulatory reporting and basic risk limits.
Regulatory Relevance: VaR and CVaR in Financial Compliance
Value at Risk (VaR) and Conditional Value at Risk (CVaR) are critical metrics in regulatory compliance for financial institutions, guiding capital adequacy and risk management standards under Basel III frameworks. VaR quantifies the maximum potential loss over a specified time at a given confidence level, while CVaR provides a more comprehensive risk assessment by averaging losses beyond the VaR threshold, capturing tail risk more effectively. Regulatory bodies increasingly emphasize CVaR for stress testing and capital reserve calculations due to its sensitivity to extreme market events, enhancing the robustness of financial risk controls.
Computational Approaches: Calculating VaR and CVaR
Value at Risk (VaR) is commonly calculated using historical simulation, variance-covariance, and Monte Carlo methods, providing a quantile-based risk estimate for portfolio losses under typical market conditions. Conditional Value at Risk (CVaR), also known as Expected Shortfall, extends beyond VaR by estimating the average loss exceeding the VaR threshold, often computed through Monte Carlo simulations and optimization techniques to capture tail risk more accurately. Advanced computational approaches leverage stochastic modeling and scenario analysis to enhance the precision and robustness of VaR and CVaR estimates in complex, high-dimensional portfolio contexts.
Choosing the Right Metric: When to Use VaR or CVaR
Value at Risk (VaR) quantifies the maximum potential loss at a given confidence level over a specific time horizon but fails to capture tail risk beyond that threshold. Conditional Value at Risk (CVaR), also known as Expected Shortfall, provides a more comprehensive risk assessment by measuring the expected loss exceeding the VaR, making it crucial for portfolios with fat-tailed distributions or significant tail dependencies. Choosing between VaR and CVaR depends on an institution's risk appetite, regulatory requirements, and the need for sensitivity to extreme loss scenarios.
Important Terms
Tail risk
Tail risk represents the probability of extreme losses in the distribution's tails beyond the Value at Risk (VaR) threshold, often underestimated by VaR which only measures potential loss at a specific confidence level. Conditional Value at Risk (CVaR) provides a more comprehensive risk assessment by calculating the expected loss exceeding the VaR, capturing the severity of tail events and enhancing risk management accuracy.
Loss distribution
Loss distribution quantifies the probability of different financial losses, essential for calculating Value at Risk (VaR) which estimates the maximum loss at a given confidence level. Conditional Value at Risk (CVaR) extends this by measuring the expected loss exceeding the VaR threshold, providing a more comprehensive risk assessment in tail scenarios.
Risk measure coherence
Risk measure coherence requires properties like subadditivity, monotonicity, and positive homogeneity, which Value at Risk (VaR) often fails to satisfy due to its lack of subadditivity, leading to potential underestimation of portfolio risk. Conditional Value at Risk (CVaR), also known as Expected Shortfall, is a coherent risk measure that addresses VaR's limitations by accounting for the tail loss distribution, providing a more reliable assessment of extreme risks in financial portfolios.
Expected shortfall
Expected Shortfall (ES), also known as Conditional Value at Risk (CVaR), measures the average loss exceeding the Value at Risk (VaR) threshold, providing a more coherent risk assessment by capturing tail risk beyond the VaR cutoff. Unlike VaR, which only indicates the maximum loss not exceeded with a certain confidence level, ES evaluates the severity of losses in the worst-case scenarios, making it essential for robust financial risk management and regulatory compliance.
Confidence level
Confidence level in Value at Risk (VaR) quantifies the probability that potential losses will not exceed a specified threshold, commonly set at 95% or 99%, whereas Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR at the same confidence level, providing a more comprehensive risk assessment of tail-end losses. CVaR offers a coherent risk metric by capturing the average of losses beyond the VaR cutoff, making it particularly useful in managing extreme market downside scenarios.
Quantile
Quantile represents the threshold below which a given percentage of data points fall, crucial for calculating Value at Risk (VaR), which estimates the maximum potential loss at a specific confidence level. Conditional Value at Risk (CVaR) extends this by averaging losses exceeding the VaR quantile, providing a more comprehensive risk assessment of extreme tail events in financial portfolios.
Fat tails
Fat tails in financial return distributions increase the likelihood of extreme losses, making Value at Risk (VaR) estimates less reliable during tail events. Conditional Value at Risk (CVaR) accounts for these fat tails by measuring the expected loss beyond the VaR threshold, providing a more comprehensive risk assessment for heavy-tailed distributions.
Scenario analysis
Scenario analysis evaluates potential losses under specific market conditions, enhancing the understanding of Value at Risk (VaR) by illustrating possible portfolio outcomes. Conditional Value at Risk (CVaR) extends this by quantifying the expected loss beyond the VaR threshold, offering a more comprehensive risk measure in extreme scenarios.
Regulatory capital
Regulatory capital requirements based on Conditional Value at Risk (CVaR) provide a more comprehensive risk measure by capturing tail risk beyond the Value at Risk (VaR) threshold, enhancing financial institutions' resilience to extreme market events.
Portfolio downside
Portfolio downside risk measures potential losses, with Value at Risk (VaR) estimating the maximum loss over a specific time frame at a given confidence level, while Conditional Value at Risk (CVaR) assesses the expected loss exceeding the VaR threshold, providing a more comprehensive view of tail risk in extreme market conditions. CVaR is preferred in risk management for its sensitivity to the magnitude of losses beyond the VaR cutoff, enhancing portfolio downside risk assessment.
value at risk vs conditional value at risk Infographic
 moneydif.com
moneydif.com