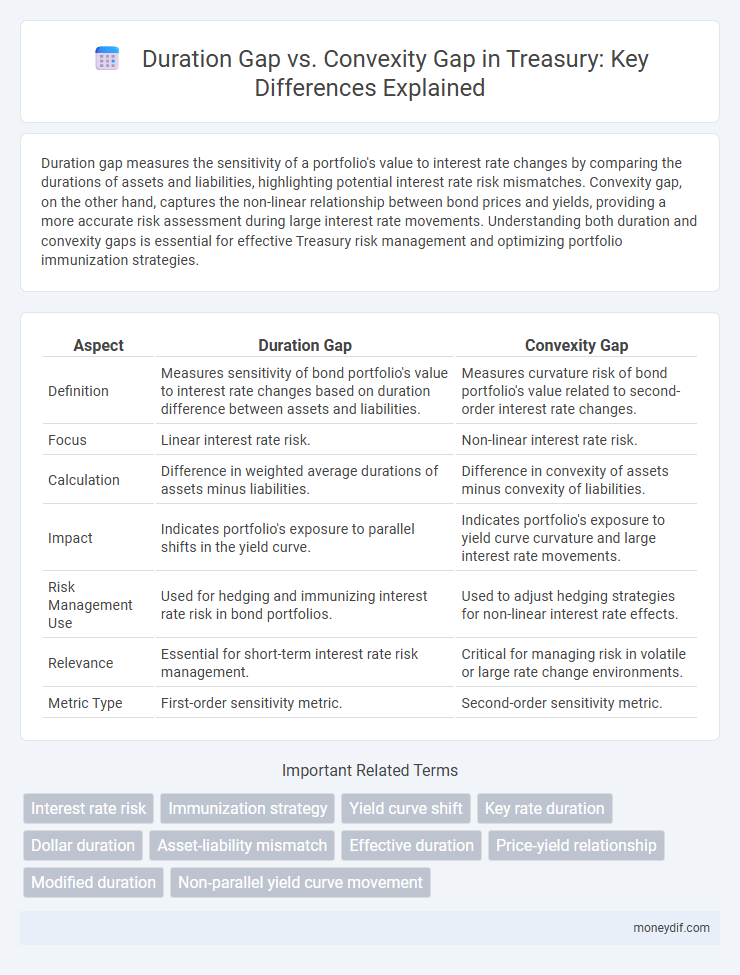
Duration gap measures the sensitivity of a portfolio's value to interest rate changes by comparing the durations of assets and liabilities, highlighting potential interest rate risk mismatches. Convexity gap, on the other hand, captures the non-linear relationship between bond prices and yields, providing a more accurate risk assessment during large interest rate movements. Understanding both duration and convexity gaps is essential for effective Treasury risk management and optimizing portfolio immunization strategies.
Table of Comparison
| Aspect | Duration Gap | Convexity Gap |
|---|---|---|
| Definition | Measures sensitivity of bond portfolio's value to interest rate changes based on duration difference between assets and liabilities. | Measures curvature risk of bond portfolio's value related to second-order interest rate changes. |
| Focus | Linear interest rate risk. | Non-linear interest rate risk. |
| Calculation | Difference in weighted average durations of assets minus liabilities. | Difference in convexity of assets minus convexity of liabilities. |
| Impact | Indicates portfolio's exposure to parallel shifts in the yield curve. | Indicates portfolio's exposure to yield curve curvature and large interest rate movements. |
| Risk Management Use | Used for hedging and immunizing interest rate risk in bond portfolios. | Used to adjust hedging strategies for non-linear interest rate effects. |
| Relevance | Essential for short-term interest rate risk management. | Critical for managing risk in volatile or large rate change environments. |
| Metric Type | First-order sensitivity metric. | Second-order sensitivity metric. |
Introduction to Duration Gap and Convexity Gap
Duration gap measures the sensitivity difference between the asset and liability portfolios to interest rate changes, quantifying interest rate risk exposure in a treasury portfolio. Convexity gap assesses the curvature difference in the price-yield relationship between assets and liabilities, capturing the non-linear effects of interest rate fluctuations. Both metrics are essential for managing and hedging interest rate risk in financial institutions.
Understanding Duration in Treasury Management
Duration measures the sensitivity of a bond portfolio's value to interest rate changes, serving as a key risk metric in Treasury management for assessing interest rate exposure. The duration gap represents the difference between the duration of assets and liabilities, indicating potential vulnerabilities to interest rate fluctuations and liquidity risk. Convexity gap complements duration analysis by capturing nonlinear price changes, enhancing the precision of risk management strategies in volatile interest rate environments.
What Is Duration Gap?
Duration gap measures the difference between the sensitivity of a financial institution's assets and liabilities to interest rate changes, reflecting the risk of changes in net worth due to rate fluctuations. It quantifies the mismatch in the timing of cash flows, helping treasurers manage interest rate risk by ensuring that asset durations align closely with liability durations. Unlike convexity gap, which considers the curvature of the price-yield relationship, duration gap primarily addresses linear interest rate sensitivity.
Defining Convexity and the Convexity Gap
Convexity measures the sensitivity of a bond's duration to changes in interest rates, capturing the curvature of the price-yield relationship beyond the linear approximation provided by duration. The convexity gap arises when the difference between the convexity of assets and liabilities leads to nonlinear interest rate risk exposure, affecting the accuracy of duration-based hedging strategies. Managing the convexity gap is crucial for Treasury risk management to ensure that portfolio value changes remain predictable under varying yield curve movements.
Key Differences Between Duration Gap and Convexity Gap
Duration gap measures the sensitivity of a bond portfolio's value to interest rate changes by comparing the weighted average duration of assets and liabilities, capturing linear interest rate risk. Convexity gap quantifies the difference in curvature between assets and liabilities' price-yield relationship, reflecting the portfolio's exposure to non-linear interest rate movements. Unlike duration gap, which assumes a linear approximation, convexity gap accounts for changes in duration as interest rates change, providing a more comprehensive risk assessment in treasury management.
Impact of Interest Rate Changes on Duration and Convexity Gaps
Duration gap measures the sensitivity of a portfolio's value to interest rate changes by comparing the duration of assets and liabilities, showing potential mismatches in interest rate risk exposure. Convexity gap further refines this analysis by accounting for the curvature in price-yield relationships, capturing nonlinear effects of large interest rate shifts. Changes in interest rates affect duration gaps by altering the timing and magnitude of cash flows, while convexity gaps impact portfolio value through second-order price adjustments, making convexity crucial for managing risk during volatile rate environments.
Measuring and Calculating Duration Gap
Duration gap measures the sensitivity of a treasury portfolio's value to interest rate changes by comparing the weighted average duration of assets and liabilities. It is calculated as the difference between the duration of assets multiplied by their market value and the duration of liabilities multiplied by their market value, divided by the total market value of equity. Convexity gap, on the other hand, quantifies the difference in the curvature of price-yield relationship between assets and liabilities but does not replace the fundamental duration gap calculation.
Measuring and Calculating Convexity Gap
Convexity gap is measured by analyzing the difference in convexity between assets and liabilities, reflecting how changes in interest rates non-linearly affect portfolio value. Calculating the convexity gap involves computing the weighted average of convexities for all instruments, then subtracting the liability convexity from asset convexity to gauge interest rate risk exposure. This metric complements duration gap by capturing the curvature in price-yield relationships, providing a more accurate assessment of interest rate sensitivity.
Risk Management Applications in Treasury: Duration Gap vs Convexity Gap
Duration gap measures the sensitivity of a treasury portfolio's value to interest rate changes by comparing the weighted average duration of assets and liabilities, aiding in interest rate risk management. Convexity gap captures the non-linear relationship between bond prices and yields, allowing treasurers to assess and mitigate risks from large or unexpected rate movements more accurately. Effective risk management in treasury requires balancing duration and convexity gaps to minimize portfolio value volatility and enhance hedging strategies under varying market conditions.
Best Practices for Managing Duration and Convexity Exposures in Treasuries
Effective treasury management requires closely monitoring the duration gap to measure interest rate risk and align asset-liability sensitivity. Managing convexity gap involves understanding the curvature of price-yield relationships, enabling better hedging against non-linear interest rate movements. Best practices include regular scenario analysis, dynamic rebalancing of portfolios, and employing derivatives to optimize both duration and convexity exposures.
Important Terms
Interest rate risk
Interest rate risk is significantly influenced by the duration gap, which measures the sensitivity difference between assets and liabilities to interest rate changes, while the convexity gap accounts for the curvature in the price-yield relationship, providing a more accurate assessment of potential bond price volatility. Managing both duration and convexity gaps is essential for financial institutions to minimize the impact of fluctuating interest rates on portfolio value and net interest income.
Immunization strategy
Immunization strategy in bond portfolio management minimizes interest rate risk by aligning the portfolio's duration with the investment horizon, effectively addressing the duration gap that measures sensitivity to parallel shifts in the yield curve. Convexity gap complements this approach by capturing the curvature effect of interest rate changes, ensuring more accurate protection against non-linear price fluctuations beyond simple duration matching.
Yield curve shift
The yield curve shift impacts bond portfolio risk by altering duration gap and convexity gap, where duration gap measures linear price sensitivity and convexity gap accounts for curvature in price changes.
Key rate duration
Key rate duration measures interest rate risk at specific maturities, highlighting sensitivity variations across the yield curve and enabling precise gap analysis. Duration gap compares overall portfolio duration to liabilities, while convexity gap accounts for the curvature in price-yield relationships, capturing nonlinear interest rate changes beyond what duration gap reveals.
Dollar duration
Dollar duration quantifies a bond's price sensitivity to interest rate changes by multiplying its duration by its market value, while duration gap measures the mismatch between assets and liabilities' durations, and convexity gap captures differences in curvature sensitivity to interest rate shifts, with both gaps influencing interest rate risk management strategies.
Asset-liability mismatch
Asset-liability mismatch occurs when the durations of assets and liabilities differ, resulting in a duration gap that exposes a firm to interest rate risk, as changes in interest rates impact the value of assets and liabilities differently. The convexity gap further refines this risk measurement by capturing the nonlinear relationship between interest rate changes and the present value of cash flows, providing a more accurate assessment of potential mismatches in interest rate sensitivity.
Effective duration
Effective duration measures a bond's price sensitivity to interest rate changes, highlighting risks better than duration gap and convexity gap by accounting for embedded options and non-linear price-yield relationships.
Price-yield relationship
The price-yield relationship in bonds is influenced by duration gap measuring linear interest rate sensitivity and convexity gap capturing the curvature effect, with convexity providing a more accurate estimate of price changes for larger yield shifts.
Modified duration
Modified duration quantifies bond price sensitivity to interest rate changes, while the duration gap measures the mismatch between asset and liability durations, and the convexity gap assesses the difference in curvature effects on portfolio value due to interest rate fluctuations.
Non-parallel yield curve movement
Non-parallel yield curve movements cause discrepancies between the duration gap and convexity gap of a bond portfolio, as duration assumes parallel shifts while convexity accounts for curvature and changing sensitivities across maturities. This mismatch can lead to inaccurate interest rate risk assessments, making convexity essential for managing portfolios exposed to varying yield curve shifts.
Duration gap vs Convexity gap Infographic
 moneydif.com
moneydif.com